Dear all,
I’m trying to implement a temperature dependent material. The reason can be found here.
The young’s modulus and poisson’s ratio for each element is given and I want to define just one material and a lot of temperatures which leads (approximately) to the given poisson ratios/youngs modulus.
I think this can be done quite easy…(at 0 K and 5 K, this makes physically no sense, but just for testing)
*MATERIAL,NAME=T_dependent_mat
*ELASTIC
210000,0.3,0
10000,0.5,5
*INITIAL CONDITIONS,TYPE=TEMPERATURE
Node_set1,0
Node_set2,5
Node_set3,3
…
*SOLID SECTION,MATERIAL=T_dependent_mat,ELSET=Eall
The ratio/modulus at my setting is given element wise, but I just can find the possibility to define the temperature at nodes. Is there a easy way to define a temperature for an element?
Additionally I would like to visualize the resulting youngs modulus in a colormap. I haven’t found a possibility at the documentation to do that. Is there a possibility to get the values of the young’s modulus for each element?
Best regards,
Patrick
As to element-wise definitions, the hardcore approach would be to explode the mesh such that each element is an unconnected mesh and re-establish connectivity by equations.
There is a script for doing this in my github example collection: https://github.com/mkraska/CalculiX-Examples/tree/master/Linear/Separate
The intent was to suppress nodal averaging of element results.
1 Like
Thanks for your help. Before I try out the hardcore approach, I want to have a look at another idea.
I want to calculate the temperature at each node in a way that the resulting poisson’s ratios match the given value. I wrote different algorithms to do this, and they work reasonable, but I’m not sure how ccx does the temperature calculation for an element.
A simple example:
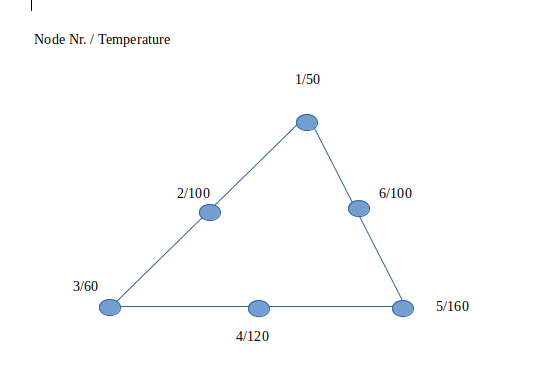
I guess ccx converts these six given temperatures to one temperature and assign this temperature to the element. With this single temperature the poisson ratio and youngs modulus is calculated depending on the defined temperature dependent material. Is this correct and is the resulting value the mean value of the six temperatures?
The material behaviour is evaluated at the integration points of an element. Where they are and how many depends on the integration scheme, you find this in the element reference of ccx or in most FEA textbooks.
The temperatures at the integration points are interpolated between the nodes using the shape functions. Thus, as long as adjacent elements share the same nodes (not like in the separeted case) you have continuous distribution of temperature throughout the structure. This continuous distribution is sampled at the integration points. If you use a user material with internal variables (depvar) you can specify initial conditions at the integration points for these variables. Then let your elastic properties depend on these variables and keep them untouched. Then their use is just for conveying values on a by integration point base.
Specifying initial temperatures for the integration points would be most straightforward but if I recall correctly, you only can specify them at the nodes, just like displacements. However, doublecheck this in the handbook (command *initial condition).
I experimented a little bit with temperature dependent materials and I got results which I do not understand. Maybe someone can help me.
Its a simple beam, fixed on one side and a force on the other side. All three cases have the same mesh and boundary conditions. The idea was to manipulate the youngs modulus with a temperature inital condition.
- I defined one material and one solid section as shown below, no temperature definition
*Material, Name=Material-1
*Elastic
20000, 0.3
*Solid section, Elset=Solid_Part-1, Material=Material-1
Maximum Displacement: 8.74e-4 mm what is really close at the analytical value (8.8e-4 mm)
- Temperature dependent Material with the same youngs modulus
*Material, Name=Material-1
*ELASTIC
20000.0,0.3, 0
20000.0,0.3, 300
*INITIAL CONDITIONS,TYPE=TEMPERATURE
1,150
2,150
3,150
and so on (for all nodes definded)
Maximum Displacement: 8.74e-4 mm what I have expected
- Temperature dependent Material with the different youngs modulus
*Material, Name=Material-1
*ELASTIC
30000.0,0.3, 0
10000.0,0.3, 300
*INITIAL CONDITIONS,TYPE=TEMPERATURE
1,150
2,150
3,150
and so on (for all nodes defined)
Maximum Displacement: 6.81e-4 mm
- Temperature dependent Material with the different youngs modulus but I changed the temperature boundaries
*Material, Name=Material-1
*ELASTIC
30000.0,0.3, 300
10000.0,0.3, 0
*INITIAL CONDITIONS,TYPE=TEMPERATURE
1,150
2,150
3,150
and so on (for all nodes defined)
Maximum Displacement: 5.83e-4 mm
I have two questions:
-Why are the results of case 3 and 2 different? I think there should be a linear interpolation thus the resulting youngs modulus should be 20000 (or is there a influence because of the basis functions and interpolation at the integration points)
A analytical calculation shows, that calculix uses a young modulus of 26000 for the beam. Why 26000 and not 20000? I would suppose 150 K would lead to a young modulus of 20000 because of my definition
-Why is there a difference between case 3 and 4? I just changed the sign of the gradient of the temperature definition. I think its due to the fact, that calculix does not use the middle of the defined temperature gradient, but why is this the case?
