Buckling of sphere

[bern]

Hi again,

I forgot two more important issues:

• in your case (pressure on outer surface) the pressure loading will always act perpendiclarly onto the buckled surface (even after buckling). Thus your loading changes direction during buckling. CalculiX does, as far as I know, not take that into account. Therefore ccx yields higher buckling stresses than what you get from the formulas (even if mesh is fine enough!). Abaqus and Ansys for instance know about that; they have got the “load stiffness effects” included.

For example a circular ring has smallest pcrit=3EI/R^3 with load stiffness included; that is what you find in all the textbooks. As far as I remember you will get 4EI/R^3 when load stiffness is ignored: Factor of 4/3 in that case!

However you know that for buckling cases you should use quite high safety margins anyway…

• Make shure you have really fine meshes that are able to model the buckling lobes correctly.

Best regards

OEB

[dichtstoff]

Hello,

i think i have done a big step, with the help of bern.
he provide me his shell mesh. i don’t get it fixed
with shell elements, but with extruded shell elements
it works fine, with simple symmetric cylindrical boundary:

first buckling mode / shape:

second buckllng mode / shape:

and now we fix beautiful 360° rings

[Paul18fr]

wonderful study (very inspiring modeling); I guess you’re using a single element on the thickness to limit the size of the model

[dichtstoff]

in my calc. of buckling mode of a spherical shell,
i get as result the expected buckling shape,
if i calc. 6 or more Number of buckling factors:
how can i avoid these ?
i think the result approach the crictial buckling shape,
more buckling facktor i use? why?

E I G E N V A L U E    N U M B E R     1
1   0.2518852E+02
E I G E N V A L U E    N U M B E R     2
1   0.2375867E+02
E I G E N V A L U E    N U M B E R     3
1   0.2359911E+02
E I G E N V A L U E    N U M B E R     4
1   0.2356157E+02
E I G E N V A L U E    N U M B E R     5
1   0.2354724E+02
E I G E N V A L U E    N U M B E R     6
1   0.2349839E+02 * waves
E I G E N V A L U E    N U M B E R     7
1   0.2346934E+02 * waves
E I G E N V A L U E    N U M B E R     8
1   0.2346061E+02 * waves
E I G E N V A L U E    N U M B E R    24
1   0.2343812E+02 * waves

[dichtstoff]

here i have the result with C3D10 elements,
generated with stp file, netgen and

24 Number of buckling factors:

*BUCKLE, SOLVER=SPOOLES
24

[klaus.wittig]

Hello Dichtstoff, you used as mentioned only the default coons shape of surfaces. Please regard the command SHPE which is used in the “SPHERE” example on Page 180 of the latest cgx manual. This command temporally creates a NURBS and relates the given surface to it which in this case defines a sphere.

[Calc_em]

@Disla

Here examples with n=18

Nº Waves	R/t	t [mm]	Pc
18	103.49	1.93	23.7

What are the supports here ? Soft springs or 3-2-1 ?

[Disla]

Assuming Z as vertical Axis

I’m constraining x and y of the poles.
I have one spring on the north pole to remove rigid body on z direction.
Two opposite points in the equator and on top of Y-axis having the same x imposed with equation.
9600 S8R elements. cc 2.21 MKL

Modeling half sphere with solid enforces the equator to be a peak or a valley removing antisymmetric solutions.That could be an option if one is searching only for symmetric solutions.

[dichtstoff]

Hello Klaus,

thank you for your reply.
Yes, i’m using only coons shape of surfaces for my sphere and for my cylinder.
So i started to try to create my models with SHPE like the example on page 180.
I work with bconverged and so with caclulix_2.XX_4win files.

The command SHPE works only with newer versions,
like 2.20; 2.21. and 2.22, but not with older verions.

I prefer my geometry of quarter sphere,
because you have no limitation with mesh refinements.
Maybe it makes sense, to change the example to better
geometry, to be independent with mesh refinements.

Working with SHPE creates me problems with an erroneouses mesh.
one issue is with C3D20 elements with the midside nodes,
so i change to create C3D8 elements and then use mids to
create the midside nodes. I check if these avoid the problem.

Other problem is the amount of elements. If the amount has
a certain value, you get an erroneouses mesh, independent of
C3D8 or C3D10 elements (but only with one bodie of three)!?

with these issue, the amount of elements are limited and you get
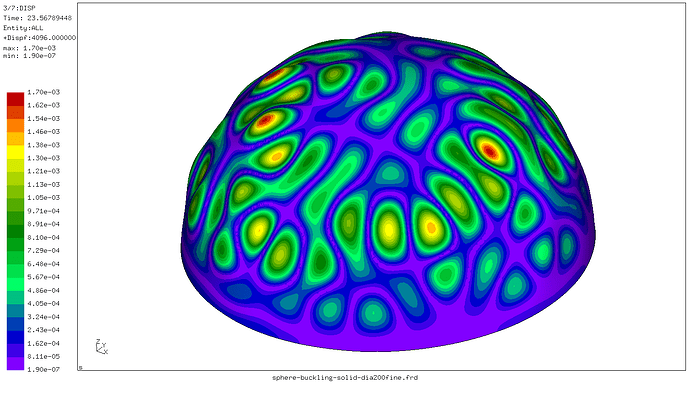
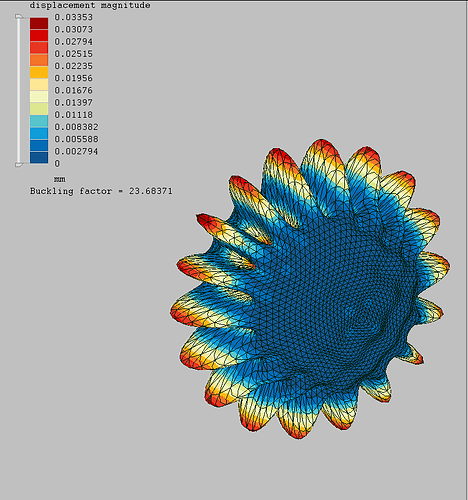
the first buckling value of 23.849, where you get no waves for buckling,
cause the value must be less than the calc. of 23.671.
So, if you change now to reduces elements, the value lowered to the calc.
value and you get in direction of the waves buckling with 23,396.

i created one more model with my working bodie, with no limit of elements
refinement, rotate only the elements a third of the quarter shape,
then rotate two times to get a quarter shpere and then create half like before.
These works also fine, but has no big influence of the buckling value and shape.
Maybe the mesh is not consisten enough.

I’ll check my cylinder model if there is a difference between BLEND and SHPE.
thnx for your reply, helped me a lot.

wbr dichtstoff

creating-sphere-solid-part.fbd

 # written by dichtstoff
 # buckling Spherical shell
 # sigma critical according Theory of elastic stability
 # thickness of sphere
 # valu sphth 1.93
 # radius of the sphere
 # valu sphrd 200
 # valu points of sphere 
 # valu sphv1 45.000000000
 # valu sphv2 35.264389683
 # amount of element with line division
 # valu lidiv 50
 ######################################
 valu sphth 1.93
 valu sphrd 200 
 valu sphth        * sphth  +0.5
 valu sphthoffseto + sphrd sphth 
 valu sphthoffseti - sphrd sphth
 valu sphrdn       * sphrd  -1.0
 valu lidiv 12

 PNT base     0.00000       0.00000       0.000000000
 PNT D001     0.00000       0.00000       sphthoffseto
 PNT D002     0.00000       0.00000       sphthoffseti
 PNT D003     0.00000       sphthoffseto  0.000000000
 PNT D004     0.00000       sphthoffseti  0.000000000
 PNT D005     sphthoffseto  0.00000       0.000000000
 PNT D006     sphthoffseti  0.00000       0.000000000
 PNT roty     0.00000       sphrdn        0.000000000
 PNT rotx      sphrdn       0.00000       0.000000000

 LINE ! D001 D002 1
 LINE ! D003 D004 1
 LINE ! D005 D006 1

 seta L001 l L001
 seta L002 l L002
 seta L003 l L003

 copy L001 L004 rot y 45
 copy L002 L005 rot x 45
 copy L003 L006 rot z 45

 seta roty p roty
 seta rotx p rotx

 move roty rot z  45
 move rotx rot z -45

 copy L006 L007 rot roty rotx -35.264389683

 merg p all

 LINE ! D001 D007 base 1
 LINE ! D001 D009 base 1
 LINE ! D002 D008 base 1
 LINE ! D002 D00A base 1
 LINE ! D003 D009 base 1
 LINE ! D003 D00B base 1
 LINE ! D004 D00A base 1
 LINE ! D004 D00C base 1
 LINE ! D005 D00B base 1
 LINE ! D005 D007 base 1
 LINE ! D006 D00C base 1
 LINE ! D006 D008 base 1
 LINE ! D007 D00D base 1
 LINE ! D008 D00E base 1
 LINE ! D009 D00D base 1
 LINE ! D00A D00E base 1
 LINE ! D00B D00D base 1
 LINE ! D00C D00E base 1

 seta linedivisonset l L008 L009 L00A L00B L00C L00D
 seta linedivisonset l L00E L00F L00G L00H L00I L00J
 seta linedivisonset l L00K L00L L00M L00N L00O L00P

 SHPE SPHi sph base sphthoffseti
 SHPE SPHo sph base sphthoffseto

 GSUR A001 + BLEND - L006 + L00O + L007 - L00P
 GSUR A002 + BLEND - L005 + L00M + L007 - L00N 
 GSUR A003 + BLEND - L004 + L00K + L007 - L00L  
 GSUR A004 + BLEND - L003 + L00G + L006 - L00I 
 GSUR A005 + BLEND - L003 + L00H + L004 - L00J 
 GSUR A006 + BLEND - L002 + L00C + L005 - L00E 
 GSUR A007 + BLEND - L002 + L00D + L006 - L00F
 GSUR A008 + BLEND - L001 + L008 + L004 - L00A 
 GSUR A009 + BLEND - L001 + L009 + L005 - L00B  
 GSUR A010 + SPHo - L00G + L00H + L00K - L00O 
 GSUR A011 + SPHi - L00I + L00J + L00L - L00P
 GSUR A012 + SPHi - L00E + L00F + L00P - L00N 
 GSUR A013 + SPHo - L00C + L00D + L00O - L00M
 GSUR A014 + SPHi - L00A + L00B + L00N - L00L 
 GSUR A015 + SPHo - L008 + L009 + L00M - L00K
 #GSUR A010 + BLEND - L00G + L00H + L00K - L00O 
 #GSUR A011 + BLEND - L00I + L00J + L00L - L00P
 #GSUR A012 + BLEND - L00E + L00F + L00P - L00N 
 #GSUR A013 + BLEND - L00C + L00D + L00O - L00M
 #GSUR A014 + BLEND - L00A + L00B + L00N - L00L 
 #GSUR A015 + BLEND - L008 + L009 + L00M - L00K
 GBOD B001 NORM - A005 - A001 - A003 - A011 + A004 + A010
 GBOD B002 NORM - A001 + A006 + A002 + A013 - A007 - A012 
 GBOD B003 NORM - A002 + A008 + A003 + A015 - A009 - A014

 div  linedivisonset mult lidiv

 #### HE20
 #div all mult 2
 #### HE20

 copy all all rot z 90
 copy all all rot z 180

 merg p all
 merg l all
 merg s all

 elty all HE8
 mesh all
 
 mids all gen
 
 elty all HE20R

 seta nodes n all
 enq  nodes boundary   rec _ _ 0 1
 enq  nodes monitor rec 0 0 _ 1 

 prnt se
 plot n boundary r
 send all abq
 send boundary abq nam
 send monitor abq
 plus e all

creating-sphere-solid-elements.fbd

 # written by dichtstoff
 # buckling Spherical shell
 # sigma critical according Theory of elastic stability
 # thickness of sphere
 # valu sphth 1.93
 # radius of the sphere
 # valu sphrd 200
 # valu points of sphere 
 # valu sphv1 45.000000000
 # valu sphv2 35.264389683
 # amount of element with line division
 # valu lidiv 32
 ######################################
 valu sphth 1.93
 valu sphrd 200 
 valu sphth        * sphth  +0.5
 valu sphthoffseto + sphrd sphth 
 valu sphthoffseti - sphrd sphth
 valu sphrdn       * sphrd  -1.0
 valu lidiv 32

 PNT base     0.00000       0.00000       0.000000000
 PNT D001     0.00000       0.00000       sphthoffseto
 PNT D002     0.00000       0.00000       sphthoffseti
 PNT D003     0.00000       sphthoffseto  0.000000000
 PNT D004     0.00000       sphthoffseti  0.000000000
 PNT D005     sphthoffseto  0.00000       0.000000000
 PNT D006     sphthoffseti  0.00000       0.000000000
 PNT roty     0.00000       sphrdn        0.000000000
 PNT rotx      sphrdn       0.00000       0.000000000

 LINE ! D001 D002 1
 LINE ! D003 D004 1
 LINE ! D005 D006 1

 seta L001 l L001
 seta L002 l L002
 seta L003 l L003

 copy L001 L004 rot y 45
 copy L002 L005 rot x 45
 copy L003 L006 rot z 45

 seta roty p roty
 seta rotx p rotx

 move roty rot z  45
 move rotx rot z -45

 copy L006 L007 rot roty rotx -35.264389683

 LINE ! D001 D007 base 1
 LINE ! D001 D009 base 1
 LINE ! D002 D008 base 1
 LINE ! D002 D00A base 1
 LINE ! D003 D009 base 1
 LINE ! D003 D00B base 1
 LINE ! D004 D00A base 1
 LINE ! D004 D00C base 1
 LINE ! D005 D00B base 1
 LINE ! D005 D007 base 1
 LINE ! D006 D00C base 1
 LINE ! D006 D008 base 1
 LINE ! D007 D00D base 1
 LINE ! D008 D00E base 1
 LINE ! D009 D00D base 1
 LINE ! D00A D00E base 1
 LINE ! D00B D00D base 1
 LINE ! D00C D00E base 1

 seta linedivisonset l L008 L009 L00A L00B L00C L00D
 seta linedivisonset l L00E L00F L00G L00H L00I L00J
 seta linedivisonset l L00K L00L L00M L00N L00O L00P

 SHPE SPHi sph base sphthoffseti
 SHPE SPHo sph base sphthoffseto

 GSUR A001 + BLEND - L006 + L00O + L007 - L00P
 GSUR A002 + BLEND - L005 + L00M + L007 - L00N 
 GSUR A003 + BLEND - L004 + L00K + L007 - L00L  
 GSUR A004 + BLEND - L003 + L00G + L006 - L00I 
 GSUR A005 + BLEND - L003 + L00H + L004 - L00J 
 GSUR A006 + BLEND - L002 + L00C + L005 - L00E 
 GSUR A007 + BLEND - L002 + L00D + L006 - L00F
 GSUR A008 + BLEND - L001 + L008 + L004 - L00A 
 GSUR A009 + BLEND - L001 + L009 + L005 - L00B  
 GSUR A010 + SPHo - L00G + L00H + L00K - L00O 
 GSUR A011 + SPHi - L00I + L00J + L00L - L00P
 GSUR A012 + SPHi - L00E + L00F + L00P - L00N 
 GSUR A013 + SPHo - L00C + L00D + L00O - L00M
 GSUR A014 + SPHi - L00A + L00B + L00N - L00L 
 GSUR A015 + SPHo - L008 + L009 + L00M - L00K
 #GBOD B001 NORM - A005 - A001 - A003 - A011 + A004 + A010
 GBOD B002 NORM - A001 + A006 + A002 + A013 - A007 - A012 
 #GBOD B003 NORM - A002 + A008 + A003 + A015 - A009 - A014

 merg p all

 div linedivisonset mult lidiv
 #div all mult 2

 elty all HE8
 mesh all
 
 mids all gen
 
 elty all HE20R

 seta part e all
 seta part n all

 copy part part-01 rot base D00D 120
 copy part part-02 rot base D00D 240

 seta part se part-01 part-02

 copy part part rot z 90
 copy part part rot z 180

 merg n all

 seta nodes n all
 enq  nodes boundary   rec _ _ 0 1
 enq  nodes monitor    rec 0 0 _ 1 

 prnt se
 plot n boundary r
 send all abq
 send boundary abq nam
 send monitor abq
 plus e all

sphere-buckling-solid.inp

**** written by dichtstoff
**** buckling spherical shell
**** sigma critical according Theory of elastic stability
**** by S. Timoshenko 1936
**** sigma critical = E*t²/[r²(3(1-v^2))^0.5]	23.67133
**** E = Young's modulus			210000
**** v = Poisson's ratio			0.3
**** t = thickness of the shell			1
**** r = radius of the sphere			200
**** vertical load = pi*r²p 			125664
**** vertical load cgx:		SHPE		125690		1.256901E+05
**** vertical load cgx:		BLEND		125552		1.255518E+05		

*HEADING
Model: buckling spherical shell

*INCLUDE, INPUT=all.msh
*INCLUDE, INPUT=boundary.nam

*TRANSFORM, TYPE=C, NSET=Nboundary
0,0,0,0,0,1

*MATERIAL, NAME=steel
*ELASTIC
210000, 0.3

*DENSITY
7.85e-9

*SOLID SECTION, MATERIAL=steel, ELSET=Eall

*STEP

***STATIC, SOLVER=SPOOLES

*BUCKLE, SOLVER=SPOOLES
1, 1.0e-6

*BOUNDARY
Nboundary,2,3,0

*DLOAD
**Esphsolqua,GRAV,9810.,0.,1.,0
Eall,P1,-0.5
Eall,P2,+0.5

*NODE FILE, 
U

*EL FILE,
S

*NODE PRINT, NSET=Nboundary, TOTALS=ONLY
RF

*END STEP

[Disla]

My result with fully structured second order tri Mecway shells.Similar than with ccx quads.

Expected 23.73 result 22.79.Non axisymmetric and antisymmetric result.

[Disla]

Same problem with ccx “shells” . Result 23.68. Completely different modeshape. Very sensistive problem.

[klaus.wittig]

@dichtstoff

I’ll check my cylinder model if there is a difference between BLEND and SHPE.
thnx for your reply, helped me a lot.

I have to thank you for looking so closely into the shpe command. I have to take some time to repeat your test.

[klaus.wittig]

@klaus.wittig

I have to thank you for looking so closely into the shpe command. I have to take some time to repeat your test.

Hello again,

I used your two fbd and the inp file but I could not reproduce the pictures. The deflections look a bit irregular on my side. What could be the reason?